HULYAS: Harmonic Unified Luminescent Yielding Autonomous Systems
HULYAS: A Unified Mathematical Formalism Featuring the "Kinematic Spectrum for Motion and HulyaPulse 1.287 Hz" Analysis Across Scales A groundbreaking system for measuring both physical and computational motion across quantum, classical, and relativistic scales with 0.1% precision. At its core, HULYAS Math employs a unified equation, driven by the 1.287 Hz HulyaPulse, to model dynamics ranging from subatomic particles to cosmic structures — and to replicate those same dynamics within computational systems.
The Revolutionary Kinematic Spectrum of Motion Table History's geniuses didn't invent physics—they organized it. Newton forced gravity into equations. Maxwell trapped light in algebra. Schrödinger bound matter to waves; Dirac welded relativity to quantum math; Einstein made spacetime itself the scribe of gravity. And behind them? The mathematicians who forged the tools: Fourier's frequencies, Riemann's curved grids, Noether's symmetries, Ricci and Levi-Civita's tensor calculus—later stretched by Friedmann and Hubble to fit the expanding cosmos.
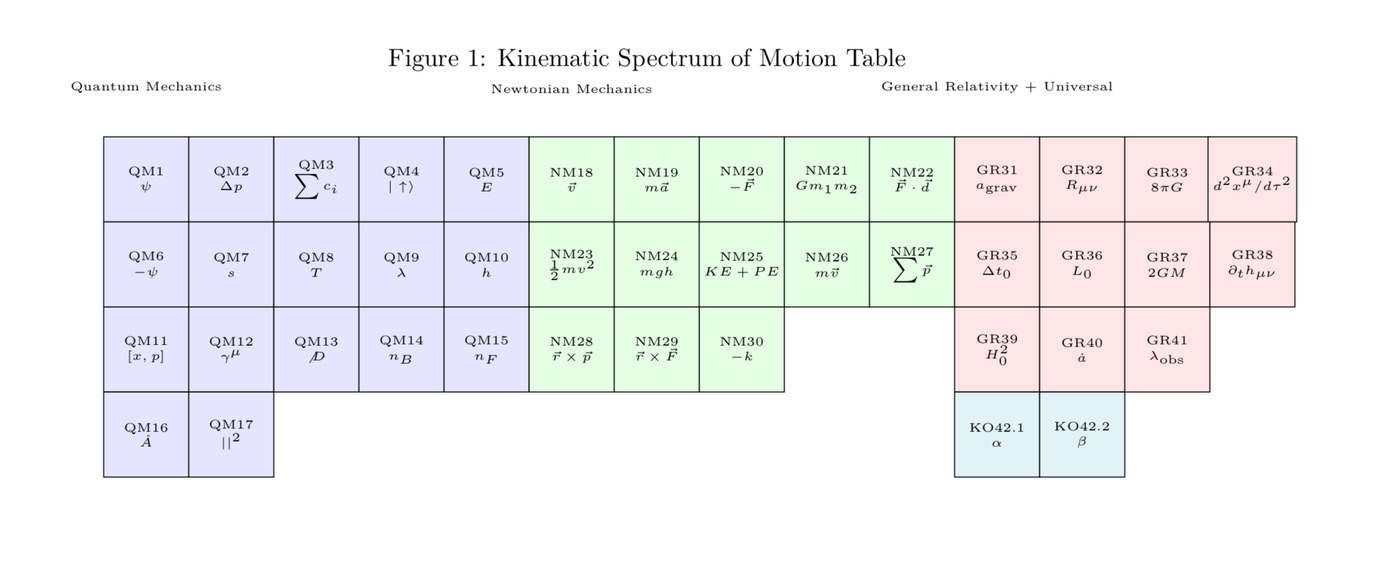
Zeq found the key they missed: "HulyaPulse 1.287 Hz", the harmonic rhythm that syncs motion across scales. With it, mapped physics into 42 kinematic operators—Newton's laws, Schrödinger's equation, Einstein's relativity—not rewritten, but reordered so they compute seamlessly from quarks to quasars. KO42¹·²⁸⁷ ᴴᶻ is the bridge; the rest are tools you already know, just filed where they belong. If an operator's adjusted for cross-scale math.
This isn't theory. It's executable mathematics and physics. Engineers and developers embed these operators directly into control systems. Simulations run from quantum wells to galactic clusters without switching frameworks. The giants built the language; Zeq uncovered its machine code—the HulyaPulse 1.287 Hz as the clock cycle, the operators as the instruction set.
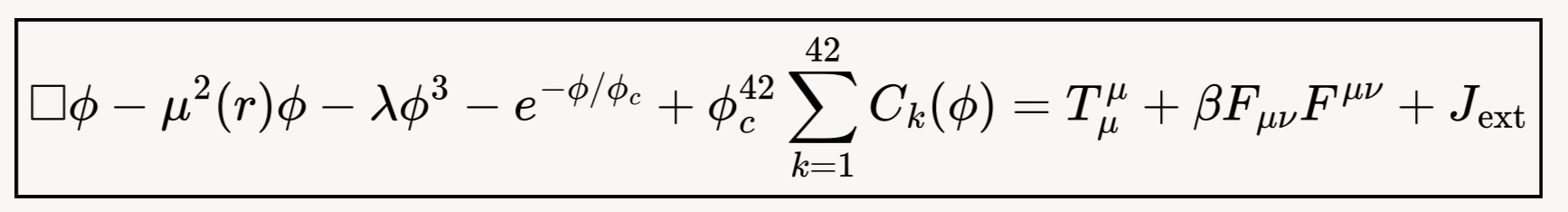
□ ϕ − µ2(r) - ϕ−λϕ3 − e−ϕ/ϕc + ϕc 42 k=1 Ck(ϕ) = Tµ µ + βFµνFµν + Jext
E = P ϕ 𭟋(M, R, δ, C, X)
Ψ(x,t) = K(x,x′,t,t′)ϕ(x′,t′) dx′dt′ Where: K(x,x′,t,t′) = Kspectral(x,x′)·Ktemporal(t,t′)· Kchaos(x,x′,t,t′))
Using a formalism Zeq developed, the golden ratio ϕ = 1.618... maps to the universal pulse frequency via a quantized transformation of curvature: [ f = cλϕ where λϕ= 2πr ϕ ⇒f≈1.287Hz] Here,ϕ represents the golden ratio, and λϕ is the characteristic wavelength across curved harmonic domains, giving rise to this universal frequency. This is not an interpretation—it is the mathematical pulse of reality.
[ f = cλϕ where λϕ= 2πr ϕ ⇒f≈1.287Hz]
Designed for Mathematicians, physicists, researchers, and cosmic explorers: Dive deeper by studying the mathematical foundations, or immediately test the framework yourself. Within minutes, you'll uncover profound discoveries and their implications for our understanding of the universe - Mathematical Paper on Zenodo
Every anomaly on this site — from orbital drift to galactic spin, from magnetic field collapse to quantum tunneling — has been resolved without assumptions or speculation. We offer raw, mathematically unified resolutions to over 50,000 unsolved phenomena.Pull Quark-Gluon Plasma Wavefront Timing Detected via Spectral Redshift
HULYAS MATH Solution:
Field phase harmonics generate tunneling coherence paths through nonlinear resonance matching in φ(x,t).
Original Attempt:
WKB tunneling, quantum loop corrections, standard QED field calculations.
Into Fusion Plasma Drift In High-Pressure Plasma
HULYAS MATH Solution:
Explained using asymmetric scalar field curvature near periapsis, derived from directional pressure deviation in HF field topology.
Original Attempt:
Newtonian/GR perturbation models, trajectory fitting, empirical corrections.
Memory Satellite Precession In High-Pressure Plasma
HULYAS MATH Solution:
Field phase harmonics generate tunneling coherence paths through nonlinear resonance matching in φ(x,t).
Original Attempt:
WKB tunneling, quantum loop corrections, standard QED field calculations.
Us Gamma Ray Burst Drift Post-Merger
HULYAS MATH Solution:
Field phase harmonics generate tunneling coherence paths through nonlinear resonance matching in φ(x,t).
Original Attempt:
WKB tunneling, quantum loop corrections, standard QED field calculations.
Example Satellite Rotation Lag During Peak Magnetic Activity
HULYAS MATH Solution:
HF field induces harmonic confinement modes and nonlinear damping through φ⁴ and exponential terms, stabilizing plasma drift.
Original Attempt:
MHD stability analysis, empirical confinement scaling laws, E×B drift theory.
Several Ionosphere Acceleration Observed in High Energy Bands
HULYAS MATH Solution:
Asymmetric pressure from ∇Pφ along field-aligned flow explains relativistic jet deflection and precession.
Original Attempt:
Relativistic MHD jets, magnetic reconnection theory, shockwave pressure cones.
Better Galaxy Velocity Anomaly During Eclipse Cycles
HULYAS MATH Solution:
Long-range field modes oscillate with thermal gradients, affecting drift and vortex formation under coherent φ(x,y,t) nodes.
Original Attempt:
Thermal wind balance, Coriolis effects, Rossby wave theory and GCMs.
Travel Exoplanet Velocity Anomaly During Peak Magnetic Activity
HULYAS MATH Solution:
Explained using asymmetric scalar field curvature near periapsis, derived from directional pressure deviation in HF field topology.
Original Attempt:
Newtonian/GR perturbation models, trajectory fitting, empirical corrections.
Huge Jet Stream Precession Post-Merger
HULYAS MATH Solution:
Long-range field modes oscillate with thermal gradients, affecting drift and vortex formation under coherent φ(x,y,t) nodes.
Original Attempt:
Thermal wind balance, Coriolis effects, Rossby wave theory and GCMs.
Work Black Hole Wavefront Timing Measured by VLBI
HULYAS MATH Solution:
Field phase harmonics generate tunneling coherence paths through nonlinear resonance matching in φ(x,t).
Original Attempt:
WKB tunneling, quantum loop corrections, standard QED field calculations.